In questo articolo vedremo alcune delle tecniche principali di Matching tra Grafi (orientati e non) e come sono state definite delle metriche di similarità tra di essi, prima di procedere però daremo delle definizioni preliminari.Definizioni preliminari sui grafiUn Grafo G (V,E) consiste di un set di vertici o nodi V, e un set di archi, E = V x V. Un grafo può essere orientato o non orientato; in un grafo non orientato, per u,v appartenenti a V, quindi (u,v) appartenenti ad E implica che (v,u) appartiene ad E.
In questo articolo vedremo alcune delle tecniche principali di Matching tra Grafi (orientati e non) e come sono state definite delle metriche di similarità tra di essi, prima di procedere però daremo delle definizioni preliminari.
Definizioni preliminari sui grafi
Un Grafo G (V,E) consiste di un set di vertici o nodi V, e un set di archi, E = V x V. Un grafo può essere orientato o non orientato; in un grafo non orientato, per u,v appartenenti a V, quindi (u,v) appartenenti ad E implica che (v,u) appartiene ad E.
Di seguito vengono illustrati i due esempi di grafi:
Per un arco (u,v), il nodo di partenza dell’arco è u e il nodo di destinazione dell’arco è v. In un grafo non orientato, entrambi i nodi u e v sono sia nodi di partenza che nodi di destinazione.
Un percorso di un grafo è una sequenza di nodi (senza ripetizione) connessa da archi. Ad esempio, 2 → 3 → 4 è un percorso ammissibile nel grafo di Figura 1, ma non per il grafo di Figura 2 perché non rispetta l’orientamento degli archi.
Un ciclo è un cammino che finisce nel suo nodo di partenza.
Un grafo è connesso se esiste un cammino tra ogni coppia di nodi. I nodi di ogni grafo possono essere partizionati in componenti connesse, ognuna delle quali è essa stessa connessa. Un grafo connesso, aciclico, non orientato è definito albero.
Una rappresentazione conveniente di un grafo è data da una matrice di adiacenza. Considerato un grafo, GA = G(VA,EA). Se la cardinalità di VA è na, allora la matrice di adiacenza A di questo grafo ha dimensione na x na nella quale l’elemento aij è uguale ad 1 se e solo se (i,j) EA, altrimenti è uguale a 0. La matrice di adiacenza di un grafo non orientato sarà sempre simmetrica. Di seguito sono riportate le matrici dei grafi delle figure 1 e 2:
 |  |
| Aa = Matrice di adiacenza del grafo Ga | Ab = Matrice di adiacenza del grafo Gb |
Ogni nodo i in un grafo ha un grado in uscita ed un grado in entrata, il primo rappresenta il numero dei nodi degli archi che partono da i mentre il secondo rappresenta il numero degli archi che terminano in i. Questi valori possono essere calcolati semplicemente sommando rispettivamente la i-esima riga e la i-esima colonna della matrice di adiacenza, per ogni nodo i. Nota che in un grafo non orientato il grado in uscita e il grado in entrata di un nodo sono uguali.
Tecniche di similarità tra grafi
Isomorfismo
Due grafi sono isomorfi se essi sono strutturalmente indistinguibili. Più formalmente, un isomorfismo è una funzione biettiva (uno a uno) tra i vertici dei grafi GA e GB:
f: V(GA) → V(GB)
con la proprietà che ogni due vertici u e v di GA sono adiacenti se e solo se f(u) ed f(v) sono adiacenti in GB. Se GA e GB sono isomorfi allora esiste una matrice di permutazione P che trasformerebbe la matrice di adiacenza A nella matrice di adiacenza B, cioè B=PAPt. Un esempio di due grafi isomorfi è riportato di seguito:
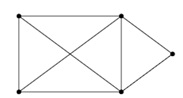 | 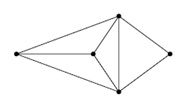 | |
| Figura 3Un grafo non orientato | Figura 4Un grafo isomorfo a quello in Figura 2.7.1 | |
Algoritmi di Isomorfismo tra Grafi
Di seguito viene data maggiore attenzione al problema noto come graph matching esatto, riportando una breve disamina di alcuni algoritmi di isomorfismo tra grafi, che sono tra quelli più citati nella letteratura informatica.
Come è ben noto, tra i differenti tipi di matching esatto (isomorfismo, graph-subgraph isomorfismo) l’isomorfismo di sottografi è un problema NP-completo, mentre è ancora una questione aperta se anche l’isomorfismo tra grafi è un problema NP-completo. Come conseguenza di ciò, i requisiti in termini di tempo nel caso peggiore aumentano esponenzialmente con la dimensione dei grafi in input, restringendo il campo di applicazione di molte tecniche basate sui grafi a grafi molto piccoli.
Algoritmi con minore complessità sono stati oggetto di ricerca negli ultimi tre decenni. Alcuni degli algoritmi proposti riducono la complessità computazionale imponendo restrizioni topologiche ai grafi (Grafi planari, Alberi, ecc..) altri algoritmi, come quello proposto da Gotlieb e Corneil [Corneil1970], trasformano i grafi in input in una rappresentazione più conveniente per il matching.
Un algoritmo molto conosciuto è quello di Ullmann [Ullmann1976], basato su una procedura di back-tracking con una funzione che “Guarda Avanti” (Look-ahead function) per ridurre lo spazio di ricerca. Questo algoritmo è stato progettato sia per l’isomorfismo tra grafi che per l’isomorfismo tra sottografi e, sebbene sia alquanto datato, è tutt’oggi uno dei più utilizzati algoritmi di graph matching grazie alla sua completezza ed efficacia.
Un algoritmo interessante che si occupa solo del problema dell’isomorfismo tra grafi è Nauty, descritto in [McKay1981], che è stato reputato essere il più veloce algoritmo per il problema dell’isomorfismo.
Di recente è stato, infine, proposto un algoritmo di matching deterministico che verifica sia l’isomorfismo tra grafi che quello tra sottografi, noto con il nome di VF Algorithm [Cordella1998,Cordella1999,Cordella2000]. L’algoritmo ha validità generale, poiché non sono imposti vincoli alla topologia dei grafi da “matchare”, e può sfruttare informazioni semantiche se disponibili. Una sua più dettagliata descrizione sarà data nel successivo Paragrafo.
VF Algorithm
L’algoritmo di base è stato sviluppato da L.P.Cordella, P.Foggia, C.Sansone, M.Vento, F.Tortorella, del Dipartimento di Informatica e Sistemistica dell’Università degli Studi di Napoli Federico II, e di seguito ne viene riportata una descrizione.
Il processo di matching tra due grafi G1 = (N1, B1 ) e G2 = (N2, B2 ) consiste nel determinare un mapping M che associa i nodi del grafo G1 a quelli del grafo G2 e viceversa. Generalmente, il mapping è espresso come un set di coppie ordinate (n,m) (con n G1 e m G2), ognuna rappresentante il mapping del nodo n di G1 con un nodo m di G2. Ogni coppia è qui denotata come componente mi del mapping M.
Lo State Space Rappresentation (da ora SSR) può essere effettivamente utilizzato per descrivere il processo di graph matching se ogni stato s del processo di matching rappresenta una soluzione parziale del mapping. Una soluzione parziale del mapping M(s) è un sub-set di M, cioè essa contiene soltanto alcune delle componenti di M. Nella rappresentazione SSR adottata una transizione tra due stati corrisponde all’aggiunta di una nuova coppia di nodi che hanno matchato.
All’inizio, le soluzioni al problema del matching possono essere ottenute computando tutte le possibili soluzioni parziali e selezionando quelle che soddisfano il tipo di matching voluto (approccio Brute Force). Allo scopo di ridurre il numero di path da esplorare durante la ricerca, per ogni stato che si trova sul percorso da s0 allo stato obiettivo (goal state) si impone che la soluzione parziale verifichi alcune condizioni coerenti al tipo di mapping desiderato. Il fondamento logico dell’algoritmo è quello di introdurre, dato uno stato s, dei criteri per prevedere se s non ha successori coerenti dopo un certo numero di passi. È chiaro che questi criteri (feasibility rules) dovrebbero permettere di trovare il più presto possibile condizioni che portano all’incoerenza. Gli stati che non soddisfano una feasibility rule possono essere scartati da successive esplorazioni.
Nella Figura 5 è schematizzato l’algoritmo proposto. Ad ogni iterazione del ciclo più esterno, l’algoritmo considera il set P(s) di coppie di nodi che possono essere aggiunte allo stato s scartando quelle coppie che non soddisfano le feasibility rules.
Ci sono due tipi di feasibility rules, che riguardano rispettivamente la sintassi e la semantica del grafo. La feasibility rule che riguarda la sintassi definita per un isomorfismo esatto è descritta in [Foggia2001]. La compatibilità semantica può essere introdotta molto semplicemente nel processo di matching: ogni qual volta un nodo del grafo G1 è comparato con un nodo del grafo G2 per determinare se una nuova coppia può essere aggiunta alla corrente soluzione parziale, gli attributi dei due nodi e degli archi che li collegano ai nodi già presenti in s sono testati semanticamente (ovviamente deve essere definito il riferimento allo specifico dominio applicativo).
L’algoritmo di matching esatto può essere esteso considerando sia le trasformazioni sulle strutture del grafo e sui nodi e gli attributi degli archi. Le trasformazioni sintattiche considerate sono lo split di un nodo in un sottografo, il merge di un sottografo in un nodo e l’inserimento o cancellazione di un arco.
Le trasformazioni sintattiche sono tenute in conto, durante il processo di esplorazione del grafo di ricerca, generando nuovi stati. Nell’esaminare uno stato nel processo di ricerca, l’algoritmo controlla se c’è una trasformazione sintattica che può essere applicata ad esso. Per ogni trasformazione applicata, un nuovo stato s è aggiunto al grafo SSR. I nodi coinvolti nella trasformazione sintattica sono marcati, con lo scopo di impedire di riconsiderarli nelle successive trasformazioni. Così facendo si impedisce la possibile generazione di cammini di lunghezza infinita nel grafo di ricerca, e si previene la possibilità che il grafo G2 matchi con un grafo G1 molto differente. Le condizioni che uno stato s deve osservare affinché una trasformazione possa essere applicata, dipende dal tipo di trasformazione. Per ogni tipo di trasformazione, solo i nodi in P(s) sono considerati come candidati così da assicurare, nel prossimo step dell’algoritmo, i nodi generati dalla trasformazione saranno testati usando le feasibility rules. In questo modo, se i nuovi percorsi sono senza risultato, essi saranno eliminati appena possibile.
Edit Distance
La ricerca di un isomorfismo tra grafi potrebbe fallire non appena vi sia una minima differenza strutturale tra i grafi. Sono state, quindi, sviluppate delle tecniche alternative al fine di individuare una metrica di similarità tra grafi. Una di queste è l’Edit Distance (Error correcting graph matching) tra due grafi che rappresenta il numero di edit operations (aggiunta, sostituzione e cancellazione di nodi e archi) richieste per trasformare un grafo nell’altro. C’è da notare che questo problema è una generalizzazione dell’isomorfismo poiché due grafi sono isomorfi se la loro Edit Distance è pari a 0.
Tipicamente, le edit operations hanno costi differenti e di conseguenza trovare la Edit Distance tra due grafi diventa un problema di ottimizzazione: determinare il minimo costo in termini di edit operations per trasformare un grafo nell’altro.
Minimo Comune Supergrafo e Massimo Comune Sottografo
Due generalizzazioni dell’isomorfismo tra sottografi sono le due nozioni di massimo comune supergrafo e minimo comune sottografo. Queste misure di similarità tra grafi confrontano due grafi GA e GB generandone un terzo. Il massimo comune sottografo è il grafo più grande contenuto in entrambi i grafi GA e GB.
Similarmente, il minimo comune supergrafo è il più piccolo grafo che contiene entrambi i grafi GA e GB. In [Bunke2000], si osserva che il problema di trovare un minimo comune supergrafo è equivalente a trovare un massimo comune sottografo, nel senso che gli algoritmi per l’uno possono essere facilmente modificati per trovare l‘altro.
La ricerca del massimo comune sottografo è un problema noto per essere NP-completo, cosicché molti algoritmi basati su detto algoritmo, hanno una complessità in termini di tempo che aumenta esponenzialmente con la dimensione dei grafi in input nel caso peggiore.
Infatti, trovare il massimo comune sottografo è equivalente ad un altro problema teorico sui grafi. Per definirlo bisogna definire il product graph GAB tra i due grafi GA e GB. Il set di nodi di GAB è VA x VB con un arco ((a,b),(c,d)) esistente se e solo se (a,c) è un arco di GA e (b,d) è un arco di GB. Detto ciò, si definisce un clique di GAB come un subset dei suoi vertici cosicché ogni vertice nel clique è connesso a tutti gli altri nel clique. Allora trovare il massimo comune sottografo tra GA e GB è equivalente a trovare il massimo clique nel product graph.
Algoritmi per la ricerca del Massimo Comune Sottografo
Gli algoritmi per la ricerca del massimo comune sottografo si dividono essenzialmente in due famiglie:
- Algoritmi che utilizzano una strategia basata sul backtracking;
- Algoritmi che determinano un association graph tra i due grafi sotto esame e poi ricercano il suo massimo clique.
Nel prossimo paragrafo esamineremo l’algoritmo di McGregor che segue il primo approccio.
McGregor Algorithm
Questo algoritmo può essere descritto adeguatamente facendo uso di una Rappresentazione tramite Spazio di Stato. Ogni stato s rappresenta un sottografo comune tra i due grafi che è in costruzione. Questo sottografo comune è una parte del massimo comune sottografo che si sta cercando. In ogni stato, una coppia di nodi non ancora analizzata (n1, n2), il primo appartenente al primo grafo e il secondo appartenente al secondo grafo, è selezionata (finché ne esiste una) attraverso la funzione NextPair(s, n1, n2). La coppia di nodi analizzata attraverso la funzione IsFeasiblePair(s, n1, n2) che controlla se è possibile espandere il sottografo comune, rappresentato dallo stato corrente, aggiungendovi questa coppia, così da ottenere un sottografo più grande. Se l’estensione è possibile, allora la funzione AddPair(n1, n2) aggiunge alla soluzione corrente la coppia (n1, n2). Dopo ciò, se lo stato corrente s non è una foglia nell’albero di ricerca, cioè esiste almeno un nodo che si riferisce al primo grafo che non è stato ancora selezionato attraverso la funzione NextPair, allora questo nodo viene selezionato ed inizia l’analisi di un nuovo stato. Dopo che il nuovo stato è stato analizzato, viene chiamata una funzione di backtrack, per ripristinare il sottografo comune dello stato precedente e per selezionare un differente stato. Usando questa strategia di ricerca, quando si sceglie un ramo dell’albero di ricerca, esso viene seguito in profondità finché non si incontra una foglia o finché una condizione di pruning si verifica.
Il primo stato è lo stato vuoto, nel quale nessun nodo ha ancora matchato. Uno pseudocodice dell’algoritmo di McGregor è mostrato in Figura 6, mentre un’applicazione dello stesso algoritmo è mostrata in Figura 7.
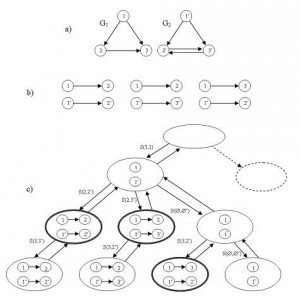
Figura 7: a) due grafi diretti G1 e G2; b) tre massimi comuni sottografi tra G1 e G2; c) una parte dell’albero di ricerca esplorato dall’algoritmo di McGregor.
Metriche di distanza tra grafi
In questo paragrafo si riportano alcune metriche di distanza tra grafi, definite in base alle nozioni di Massimo Comune Sottografo e Minimo Comune Supergrafo date in precedenza.
La metrica MMCSN definita in [Schenker2005]:
dove:
- mcs (G1, G2) è il massimo comune sottografo;
- MCS (G1, G2) è il minimo comune supergrafo.
La metrica MCS definita in [Bunke1998]:
La metrica WGU definita in [Wallis2001]:
![]()
La metrica UGU definita in [Bunke1997]:
Infine la metrica MMCS definita in [Fernàndez2001]:
Riferimenti:
[Bunke1997] H. Bunke, “On a relation between graph edit distance and maximum common subgraph”, Pattern Recognition Letters, Vol. 18, 1997.
[Bunke1998] Horst Bunke, Kim Shearer, “A graph distance metric based on the maximal common subgraph“ Institut fur Informatik und angewandte Mathematik, University of Bern, Bern, Switzerland Department of Computer Science, Curtin University of Technology, Perth, WA, Australia Received 22 July 1998.
[Bunke2000] H. Bunke, X. Jiang, A. Kandel, “On the minimum common supergraph of two graphs“ Computing, v. 65, 13-25, 2000.
[Corneil1970] D.G. Corneil, C.C. Gotlieb, “An efficient algorithm for graph isomorphism“, Journal of the Association for Computing Machinery, 17, pp. 51-64, 1970.
[Cordella1998] L.P. Cordella, P. Foggia, C. Sansone, M. Vento, “Subgraph Transformations for the Inexact Matching of ARG.pdf“, Computing suppl. 12, pp. 43-52, 1998.
[Cordella1999] L.P. Cordella, P. Foggia, C. Sansone, M. Vento, “Performance evaluation of the VF Graph Matching Algorithm.pdf“, Proc. of the 10th ICIAP, IEEE Computer Society Press, pp. 1172-1177, 1999.
[Cordella2000] L.P. Cordella, P. Foggia, C. Sansone, M. Vento, “Fast Graph Matching for Detecting CAD Image Components“, Proc. of the 15th Int. Conf. on Pattern Recognition, IEEE Computer Society Press, vol. 2, pp. 1038-1041, 2000.
[Fernàndez2001] M.-L. Fernández and G. Valiente, “A graph distance metric combining maximum common subgraph and minimum common supergraph”, Pattern Recognition Letters, Vol. 22, 2001.
[Foggia2001] P. Foggia, C. Sansone, M. Vento, “A performance comparison of five algorithms for graph isomorphism.pdf“, Proceedings of the 3rd IAPR-TC15 Workshop on Graph based Representation (GbR2001), Italy, 2001.
[A. Schenker, “Graph-Theoretic Techniques for Web Content Mining“ A dissertation submitted in partial fulfillment of the requirements for the degree of Doctor of Philosophy Department of Computer Science and Engineering College of Engineering University of South Florida 2005.
[Ullmann1976] J.R. Ullmann, “An Algorithm for Subgraph Isomorphism“, Journal of the Association for Computing Machinery, vol. 23, pp. 31-42, 1976.
[Wallis2001] W.D. Wallis, P. Shoubridge, M. Kraetz, and D. Ray, “Graph distances using graph union”, Pattern Recognition Letters, Vol. 22, 2001.




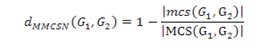

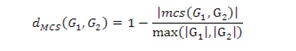
COMMENTS